Zejun Lin's Blog

异国漂泊，野蛮生长

0%

模型的评估和选择

Posted on Edited on

自从过完年后，生活变得越来越匆忙，平日里时间基本为新的论文和学习英语所占用，但仍想抽出一小部分时间复习以往学过的机器学习的知识，并做个总结。

模型评估

误差

通常，在训练一个学习器的时候，我们会将手上现有的数据按一定比例分为训练集和测试集，使用训练集去训练这个学习器，并用测试集去测试它的错误率。

  • 这里，我们把学习器
    • 在训练集上的误差称为”训练误差“(training error)或者”经验误差“(empirical error)，
    • 把其在测试集上的误差称为”泛化误差“(generalization error)

过拟合&欠拟合

对于训练集和测试集的分法，其实是有讲究的，否则便很容易造成一些问题，比如学习器在训练集上表现得很好，而在测试集却很糟糕，我们将之称为“过拟合”(overfitting)，与之相对的是“欠拟合”(underfitting)，是指即便是在训练集上，学习器也表现的不好

  • 对于过拟合，实质上是学习器过度拟合了训练数据，即对于训练数据的特征，无论好坏，一股脑全学了，而有些特征，仅仅是训练数据中特有的特性，在其他数据上并不存在这么一些特性，这就导致了学习器的泛化能力弱，在测试集上表现糟糕。

  • 这就好比你想学习追妹子，你去问你那可爱的小表妹喜欢什么样的男生，然后她告诉你她喜欢干净帅气的男生，同时她也喜欢周杰伦的歌，喜欢吃酸菜鱼吃榴莲，喜欢玩LOL…总之她告诉你一堆规则。好了，现在你安安分分地修炼，直到有一天你终于完美地符合这些规则了，训练完成。你找到个妹子超级自信地去追，然而你发现这好像没有什么卵用，妹子告你你她只喜欢干净帅气的男生，其它的她都不care，甚至，她讨厌吃辣的，觉得榴莲很臭，并且超级讨厌玩游戏的男生，接着你便gg了。在训练数据表现好，在测试数据表现糟糕，这便是过拟合了。

评估方法

留出法(hold-out)

这是最常用的方法，即将数据集D直接按一定的比例随机分为两个互斥的集合，一个作为训练集，一个作为测试集。

交叉验证法(cross validation）

这便是大名鼎鼎的CV方法了，简单来说，就是将数据集分成k个大小相似的互斥子集，然后每次选一个子集作为测试集，其他的k-1个合并作为训练集合训练模型，这样，总共便可进行k次训练和测试，最终再返回这k次测试结果的均值作为最终结果。因此，CV也被称做k折交叉验证（k-fold cross validation），其中，k的取值尤为重要。

自助法

按照前边的做法，我们训练学习器的时候，其实用的只是整个数据集的一部分，但其实我们最终想要的是用整个数据集训练出来的学习器，这难免会造成一定的偏差，特别是对于整个数据集本身就比较小的情况。

  • 自助法针对的便是这种情况，其做法是对数据集D进行采样。
  • 假设D有m个样本，其流程为
    • 不断随机选取数据集D中的一个样本
    • 拷贝后添加到另一个空数据集D’中
    • 总共重复m次
  • 最终采用D’为训练集，而D/D’为测试集。

调参与验证集

由上边我们知道，对于一个包含m个样本的数据集，最终的模型成品必定是使用这m个样本的整个数据集训练出来的，而这个模型在实际使用中遇到的数据才称为测试数据。

同时，我们知道，为了学习数据分布，一般模型都是有大量的参数需要调整的，这里便引申出来另外一个概念——验证集(validation set）。

为了与前边区分，一般把模型评估和选择中用于评估测试的数据称为验证集，用于模型选择和调参，而用测试集来评估模型在实际使用中的泛化能力。层级关系如下：

  • 整个数据集
    • 训练数据
      • 训练集
      • 验证集
    • 测试数据

性能度量

性能度量是为了对学习器的泛化性能进行评估的，衡量模型泛化能力的评价标准

均方误差

对于回归任务，最常用的是“均方误差”(mean squared error)

  • 给定:
    • 学习器f
    • 数据集$D={(x_1,y_1),(x_2,y_2),…,(x_m,y_m)}$
      • $x_i$为输入
      • $y_i$为$x_i$的真实标签，即答案
  • 则均方误差为：

错误率和精度

前面所提到的错误率和精度也是一种性能度量，既适用于二分类，也可以用于多分类，这个比较简单便不多加赘述。

查准率Precision、查全率Recall

这里先阐述一个概念，对于二分类来说，一般我们把要识别（查找）出来的类别叫做正类，其样本叫做正样本，或者正例。而把余下的那些干扰的叫做负类，样本自然叫负样本或者负例。

譬如说，对于一个学习猪脸识别的学习器来说，其输入为一张照片，倘若输出为判断照片里是否有猪脸，那么输入的照片里如果有猪脸，它就是一个正样，反之，如果照片里只是一张椅子，或者一个人这些无相关的东西，那么就是一个负样

  • 查准率，顾名思义，即你查出来的所有正例里面，是真正的正例的所占的比例有多少个，即是说，你这个学习器，它有多准。
    • 比如说，学习器查出10张有猪脸的相片，但其实这10张相片只有8张是有猪脸的，其余两张并没有出现猪脸，那么其查准率就是80%。

  • 查全率，同样的，看名字，查得有多全。即学习器所查出来的正例，占样本里总的正例的比例。

    • 比如说，我一共有100张照片，其中有50张是有猪脸的，学习器查出来有60张有猪脸的照片，但其实这60张里面只有40张照片是有猪脸的，也就是说，50张有猪脸的照片里面，学习器只挑出了40张，那么其查全率就是$40/50=80\% $。顺带一说，这个例子里其查准率为$40/60=2/3 \approx 66.7\%$

  • 在分类任务中，有个很常用的矩阵，叫做“混淆矩阵”(confusion matrix)，是以类别间的关系评价精度的一种标准格式，以二分类为例，描述的即以下四者：

    • 真正例 True Positive TP — 正确的肯定数目
    • 假正例 False Positive FP — 误报数目
    • 真反例 True Negative TN — 正确否定的数目
    • 假反例 False Negative FN — 漏报数目

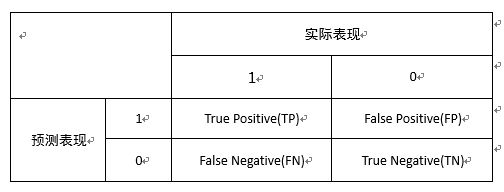
  • confusionMatrix.jpg-11.8kB

    • Precision = TP/(TP+FP)
    • Recall = TP/(TP+FN)

这样，我们便可以很方便地计算出查全率Recall和查准率Precision。

P-R曲线和F1

为什么人们要引出Recall和Precision这两个概念呢？单单Accuracy不够吗？
是的，有些时候，人们对于一个学习器侧重点的不同，导致了其关注点的不同。比如下面两种情况：

  • 自然灾害的预测
    • 对于像地震海啸之类的自然灾害的预测，人们所期望的Recall率是要很高的，即宁可预测错多几次，也要把所有灾害都给预测到，未雨绸膜也好，曲突徙薪也罢，总是没有坏处的。这时候Precision就显得不是十分重要了。
  • 嫌疑犯的定罪
    • 相反，对于另外的一些情形像嫌疑犯定罪，本着不能冤枉一个好人的原则，Precision的地位在这里就比较突出了，人们希望这里的分类器，预测出来的总是真的，即便有时recall低点（放走了罪犯），亦是值得的。

另外，对于一个二分类的学习器来说，一般它会输出每个样本属于正类的概率，这时，就需要一个Cutoff，即阈值的点来衡量了，我们把概率低于这个点的分到负类，高于这个点的分到正类。
自然地，不难发现，这个cutoff点的选取便成为了关键。对于一个学习器，分别选取不同的阈值，就会有一系列的混淆矩阵，也就会有一系列的Recall和Precision值的对，把这些对在坐标系中按照cutoff值排序后连起来，便形成了P-R曲线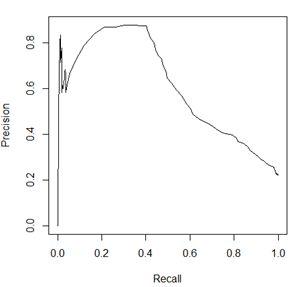
PR.jpg-6.7kB

由图可知，Recall和Precision大体上是呈负相关的，但要注意的一点是，这个曲线并不一定经过(0,1)和(1,0)这两个点。

既然Recall和Precision是负相关的关系，那么如何根据这两个量度量一个学习器的综合性能呢？有以下一些方式：

  • 平衡点 (Break-Even Point, BEP)
    • 这个很容易理解，即以当Recall=Precision时的值为衡量标准
    • 即上图曲线与直线y=x的交点
  • F1
    • 当然BEP未免过于简单，于是便衍生出了F1
    • F1是Recall和Precision的调和平均数

另外一个概念是，当学习器被应用到多个数据集上(即获得多个混淆矩阵)时，我们该如何综合考量？以下是两种衡量方法：

  • 宏F1 (Macro-F1)
    • 流程：
      • 分别计算各个混淆矩阵的Recall和Precision
      • 计算Recall和Precision的平均值
      • 根据平均值计算F1
    • 公式：
      • $\text{macro-P} = \frac{1}{n}\sum_{i=1}^{n} P_i$
      • $\text{macro-R} = \frac{1}{n}\sum_{i=1}^{n} R_i$
      • $\text{macro-F1} = \frac{1}{\frac{1}{macro-R}+\frac{1}{macro-P}}$
  • 微F1 (Micro-F1)
    • 流程:
      • 先将混淆矩阵的各个元素进行平均得到$\overline {TP},\overline{FP},\overline{TN},\overline{FN}$
      • 根据这些均值计算出Recall和Precision
      • 计算F1
    • 公式：
      • $\text{micro-R}=\frac{\overline{TP}}{\overline{TP}+\overline{FN}}$
      • $\text{micro-P}=\frac{\overline{TP}}{\overline{TP}+\overline{FP}}$
      • $\text{micro-F1} = \frac{1}{\frac{1}{micro-R}+\frac{1}{micro-P}}$

ROC和AUC

  • ROC
    • 即Receiver Operating Characteristic，“受试者工作特征”
    • 就其表示的含义，玄学地讲，该曲线上每个点（即每个阈值对应的点）反映着对同一信号刺激的感受性，即其特异性和敏感性，详细内容见下。
  • AUC
    • 即Area Under Curve，是指ROC曲线下面的面积
    • 一般在(0.5,1)区间
    • 如若为0.5，则和随机猜测没有差别
    • 如若模型十分准确，则为1

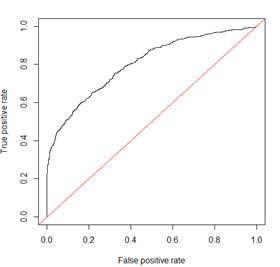
PR.jpg-6.9kB

  • 该图每个点对应一个阈值
  • 横轴：
    • FPR (False Positive Rate)
    • 1 - 特异度（Specificity）
    • 负类覆盖率
    • FPR = $\frac{FP}{FP+TN}$
    • FPR越大，预测正类中实际负类就越多
  • 纵轴：
    • TPR (True Positive Rate)
    • 灵敏度 Sensitivity
    • 正类覆盖率，其实就是召回率Recall
    • TPR = $\frac{TP}{TP+FN}$
    • TPR越大，预测正类中实际正类就越多
  • 目标:
    • TPR=1 && FPR=0，即图中(0,1)点
    • 换种说法，即曲线偏离直线y=x越大，AUC面积越大，效果越好