Linear Regression

延续上一篇关于预测理论和ML的内容，本文旨在从数学角度理解和推导线性回归。

内容主要包括：

1. 回归问题中的统计模型——从有输入到无输入模型
   1. 建模和评估风险（风险函数，损失函数等）
   2. 作出最优预测
2. 线性回归模型
   1. 线性回归是啥
   2. 数据拟合参数的方法
      1. 最大似然估计 MLE
      2. 经验风险最小化 ERM (Empirical Risk Minimization)
   3. ERM 怎么解
   4. ERM 表现评估（overfitting等内容）

一、回归问题中的统计模型

无输入模型

为了简化问题，我们同样先来看一个没有输入的回归模型，就像前文的从抛硬币事件，我们只能观察到模型不同的输出结果。不同的是，抛硬币只有两个输出结果，但在回归问题中，我们预测的是连续的实数值， 这里有个类似的装置是高尔顿板——一块竖直放置的板，上面有交错排列的钉子。让小球从板的上端自由下落，当其碰到钉子后会随机向左或向右落下，最终，小球会落至板底端的某一格子中。当格子足够多的时候，我们可以看成是连续的。

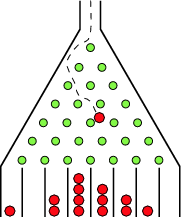
— Image from Wolfram MathWorld

我们要预测的就是球最终会落到哪个格子。

可以看到，跟抛硬币一样，小球落下的最终位置是随机，所以要先选用一个统计模型来进行建模，这里选用平均值为$\mu$，方差为$\sigma^2$的高斯分布，写作 $N(\mu, \sigma^2 )$。那么我们要怎么衡量预测结果好坏呢？这里引发了两个问题：

1. 一是在回归问题中，因为结果是连续的，我们基本不可能预测到和真实值一模一样的结果。
   • 注意到在前文中，因为预测结果只有对错两种区别，所以我们可以用错误率来衡量预测结果，其实也就是zero-one loss；
2. 二是因为输出是随机的，所以我们不能只是单看一次预测。

对应的解决方法是

1. 改用预测值和真实值的距离平方来衡量结果，叫作平方差损失 Square loss (对比zero-one loss)。
2. 计算这个Square loss的期望值，称为 期望平方差损失 Expected square loss。同样的，这个值自然是越小越好。

最优预测

整理一下上文信息，可以知道

• 真实位置 $Y$ 是一个随机变量，且$\mathbb{E}[Y] = \mu，Var[Y] = \mathbb{E}[(Y-\mathbb{E}[Y])^2] = \sigma^2$

• 我们要预测 $\hat y\in R$，且最小化期望平方差损失 $\mathbb{E}[(\hat y - Y)^2]$

拆解一下得到

$$\begin{aligned}\mathbb{E}[(\hat y - Y)^2] &= \mathbb{E}[((\hat y - \mu) + (\mu -Y))^2]\\&= \mathbb{E}[(\hat y - \mu)^2] + \mathbb{E}[(\hat y - \mu)]\cdot \mathbb{E}[(\mu -Y)] + \mathbb{E}[(\mu -Y)^2]\\&= (\hat y - \mu)^2 + \sigma^2\end{aligned}$$

这个过程叫做Bias-variance decomposition，直译应该叫偏置方差分解 ？注意到这里Y是随机变量，$\mu, \hat y$都是实值，所以中间的期望相乘可以拆开，且$\mathbb{E}[(\mu - y)] = 0$

从最终结果容易看出，为了最小化期望平方差损失 ，我们作出最优预测 $\hat y = \mu$

有输入模型

这里的线性回归模型和前文为带标签数据建立的模型[TODO: cite]基本是一样的，除了

1. 预测值变成了实数，而不是{0, 1}或者{0, 1, 2, …, K}
2. 我们更加关心平方差损失，而非预测的对错

这里引入一个概念叫作 Risk Function 风险函数，风险函数一般和某个损失函数搭配使用，用于衡量期望意义上某个预测函数的好坏。在这里，对于一个预测函数 $f$，以平方差损失为例，它的风险为

$$R(f) = \mathbb{E}_p[(f(\boldsymbol{X})-Y)^2] = \int\int p(\boldsymbol{x}, y)(f(\boldsymbol{X})-Y)^2 d\boldsymbol{x} dy$$

其中，p是 $\boldsymbol{x}, y$的原分布。

其实，错误率也是一种风险函数，只不过它的损失函数是zero-one loss，即 $\unicode{x1D7D9}_{f(x)\ne y}$。

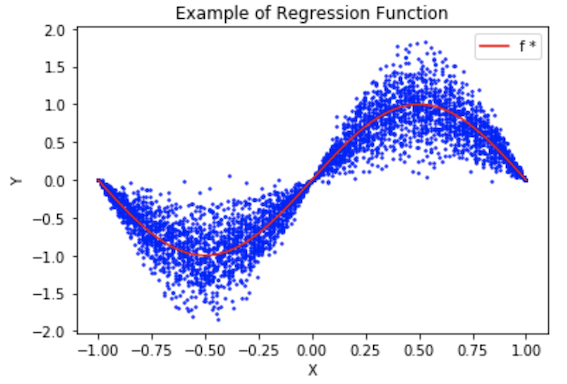
最优预测

从无输入的最优预测，我们可以看出，最优预测总是预测其期望值，因为在有输入的模型中，给定一个输入X，Y的分布就被固定下来，我们预测这个分布的期望值就行了，也就是

$$f^* = \mathbb{E}[Y|\boldsymbol{X}=\boldsymbol{x}]$$

同样的，这个函数也就做回归函数，它给出了最小分险的预测，且由给定X情况下，Y的分布决定。

二、线性回归模型

上文讲到，最优预测就是给定 $\boldsymbol{X}$ ，预测 $Y$ 的期望值，但并没有讲到如何利用 $\boldsymbol{X}$ 去预测 $Y$ 的期望值。线性回归，故名思义，就是用线性关系去拟合 $\boldsymbol{X}$ 和 $Y$ 期望值之间的关系，这里的$\boldsymbol{X}$ 指的是一个d个实数值的列向量，即$\boldsymbol{X}\in \mathbb{R}^d$。那么给定 $\boldsymbol{X}=\boldsymbol{x}$， 有 $\mathbb{E}[Y] = \boldsymbol{x}^Tw$，这里的 w 就是人们常说的权重向量。

那么，我们就讲 $(\boldsymbol{X}, Y)$ 的线性回归模型写作

• $Y|\boldsymbol{X}=\boldsymbol{x} \sim N(\boldsymbol{x}^T w, \sigma^2)$
  • 这里的假设是给定 $\boldsymbol{X}=\boldsymbol{x}, Y$的分布同上文是高斯分布，但也可以是其它以 $\boldsymbol{x}^T w, \sigma^2$ 为参数的分布
  • w 是权重向量，$\sigma$ 是分布的另外一个参数，但一般和预测无关

如无特殊说明，这里的向量均为列向量，比如上文的 x 。

对应地，$\boldsymbol{x}^T$ 是对应的行向量（即x的转置），$\boldsymbol{x}^Tw$ 可以理解为矩阵相乘，也可以理解为两个向量的点积。

即，

$$x = \begin{bmatrix}x_1\\ x_2\\ ... \\ x_d \end{bmatrix}, x^T=\begin{bmatrix}x_1, x_2, ..., x_d \end{bmatrix}\\x^Tw = \begin{bmatrix}x_1, x_2, ..., x_d \end{bmatrix} \cdot \begin{bmatrix}w_1\\ w_2\\ ... \\ w_d \end{bmatrix} = \sum_{i=1}^d x_iw_i$$

A. 增强线性回归——特征变换

一般人们为了让线性回归更加好用，不用直接使用原输入 x， 而是会对它做一个变换，用函数可以表示为 $\varphi(x)$， 然后再去和权重向量相乘，即$\varphi(x)^T w$。比如

• 非线性数值变换：$\varphi(x) = \ln (x+1)$
• 三角变换：$\varphi(x) = (1, sin(x), cos(x), sin(2x), cos(2x), …)$
• 多项式变换：$\varphi(x) = (1, x_1, x_2, …, x_d, x_1^2, x_2^2, …, x_d^2, x_1x_2, …, x_{d-1}x_d)$

这其中最重要的就是仿射变换 Affine Transformation，它相当于给线性变换加了个截距项a，写作

$$\varphi(\boldsymbol{x}) = (1, \boldsymbol{x})$$

这里的$\boldsymbol{x}$是一个向量，相当于给$\boldsymbol{x}$加多一个维度，值为1，同样将w扩展为 $w = (a, b)$， 那么 $\varphi(\boldsymbol{x})^T w = a+b\boldsymbol{x}$, 一般把a叫做截距项，即 intercept term。

为什么仿射变换特别重要呢？考虑下面这个例子，假设 y 是健康指标， x 是体温。医学研究表明和健康相关的特征是体温与 37 度的距离平方，即 $(x - 37)^2$。这里就出现一个问题了，一开始我们并不知道 37 这个数字，但加上仿射变换之后，就可以让模型自己去学习啦！

B. 拟合数据的方法

当然了，和抛硬币问题一样，现实中我们并不知道原模型分布的参数，以上文的例子来说，就是不知道 $\mu, \sigma$。所以我们需要用可观察的数据，即很多的 $(\boldsymbol{X}, Y)$ 数据点去拟合权重向量 w。

最大似然估计 Maximum Likelihood Estimation (MLE)

在上一节里面，我们用 $w^T\boldsymbol{x}$ 去估计原分布的期望值，接下来我们可以用观察到的数据去获得对权重向量 w 的最大似然估计。

给定数据 $\left(\boldsymbol{x}_{1}, y_{1}\right), \ldots,\left(\boldsymbol{x}_{n}, y_{n}\right) \in \mathbb{R}^{d} \times \mathbb{R}$，我们用MLE可以获得 $(w, \sigma^2)$ 的 log-likelihood 如下：

$$\sum_{i=1}^{n}\left\{-\frac{1}{2 \sigma^{2}}\left(\boldsymbol{x}_{i}^{\top} \boldsymbol{w}-y_{i}\right)^{2}+\frac{1}{2} \ln \frac{1}{2 \pi \sigma^{2}}\right\}+\left\{\text { 与 }\left(\boldsymbol{w}, \sigma^{2}\right)\text {无关的项}\right\}$$

那么最大化以上这个log-likelihood的 $\boldsymbol{w}$ 也就是最小化如下项的 $\boldsymbol{w}$:

$${\qquad \frac{1}{n} \sum_{i=1}^{n}\left(\boldsymbol{x}_{i}^{\top} \boldsymbol{w}-y_{i}\right)^{2}}$$

经验风险最小化 Empirical Risk Minimization (ERM)

先不管什么是ERM，回到上文风险函数的概念，若损失函数是平方差损失，那么对于一个预测函数，它的风险为

$$R(f) = \mathbb{E}[(f(\boldsymbol{X})-Y)^2]$$

我们知道期望等于以概率为权重的每个结果的累加或积分，但其实我们并不知道原分布的概率密度函数，即不知道每个样本$(\boldsymbol{X}, Y)$ 的概率。那么要怎么计算风险呢？这里引入一个(经验分布 Empirical Distribution 的概念，它是对从原分布随机可重复采样的数据的经验衡量。简单来说：

• 在 $(\boldsymbol{x}_1, y_1), …, (\boldsymbol{x}_n, y_n) $ 上的经验分布 $P_n$ 就是一个给每个样本点赋予 1/n 概率的一个分布。

其实很合理，我们不知道每个从原分布随机采样出来的$ (\boldsymbol{X}_i, Y_i)$ 数据点的概率，那就都给均等概率1/n好了，这样，如果原分布在某个区域的概率密度比较高，那么随机采样出来更多数据点的可能性高，即经验分布在该处的概率也会相应增高。

好了，这样，虽然我们没办法得到预测函数真正的风险，但我们可以利用插入原理，用经验分布 $P_n$来替代原分布 $P$，得到对真正风险的一个估计，称之为经验风险 Empirical Risk:

$$\hat R(f) = \mathbb{E}[(f(\boldsymbol{X})-Y)^2] = \frac{1}{n}\sum_{i=1}^n(f(\boldsymbol{x}_i)-y_i)^2$$

注意到这里的R头上带个符号，代表是预估的经验风险，而不是真正的风险

所以接下来的任务就是找到一个 $f$ ，使得这个经验风险最小，写到这里，读者大概会发现，ERM和MLE在线性回归模型得出的结论竟出奇的一致！

C. ERM的解决之道

对于一个线性回归方程 $f(\boldsymbol{x}) = w^T \boldsymbol{x}$， 它经验风险 Empirical Risk 本质上是什么？从几何的角度来看，如下图所示，它就是求每个采样数据点到超平面的竖直距离的平均值。那么要怎么求呢？

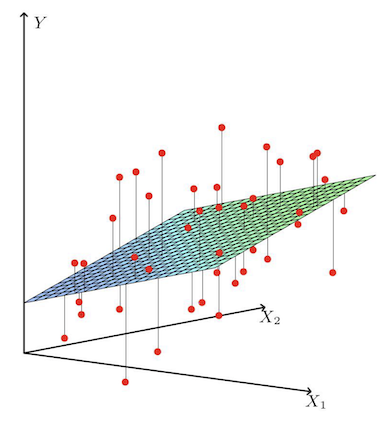
为了方便分析，我们先将ERM转换成矩阵的形式，首先是数据矩阵A和对应的标签b

$$A = \frac{1}{\sqrt{n}}\begin{bmatrix}\boldsymbol{x}_1^T\\ \boldsymbol{x}_2^T\\ ... \\ \boldsymbol{x}_n^T \end{bmatrix} \in \mathbb{R}^{n\times d} \text{ and } \boldsymbol{b} = \frac{1}{\sqrt{n}}\begin{bmatrix}y_1\\ y_2\\ ... \\ y_n \end{bmatrix} \in \mathbb{R}^{n}$$

这里有几个点需要注意一下

• 这里的 x 是粗体，代表的是一个向量(某个数据点 $\boldsymbol{X}=\boldsymbol{x}$)，我们默认假设总共有n个点，每个点的 x 的维度是d，即 $\boldsymbol{x} \in \mathbb{R}^d$， 所以A是一个 n行d列的数据矩阵。
• 前面的系数 $\frac{1}{\sqrt{n}}$ 只是一种定义的选择，纯粹是为了后续计算方便，因为这样 Ab 就能生成一个 $\frac{1}{n}$ 的项，与ER中的 $\frac{1}{n}$ 对应。

那么，经验风险就可以表示为：

$$\hat R(f) = \frac{1}{n}\sum_{i=1}^n(f(\boldsymbol{x}_i)-y_i)^2 = ||\boldsymbol{Aw-b}||_2^2$$

对于一个向量 v， $||\boldsymbol{v}||_2$ 代表它的 l2-norm)，其等于 v 所有元素的平方和的开根，即$||\boldsymbol{v}||_2 = \sqrt{\sum \boldsymbol{v}_i^2}$

求权重向量 w 是的经验风险最小的方法有很多种，这里介绍下最简单粗暴的直接求导，即令$\nabla \hat R(\boldsymbol w) = 0$：

简单推到如下：

首先，注意到 $\boldsymbol{Aw-b}$ 的结果是一个列向量，那么它 l2-norm 的平方就等于它和自身的乘积：

$$\hat R(\boldsymbol w) = ||\boldsymbol{Aw-b}||_2^2 = (\boldsymbol{Aw-b})^T (\boldsymbol{Aw-b})$$

所以倒数为

$$\nabla \hat R(\boldsymbol w) = \frac{d (\boldsymbol{Aw-b})^T (\boldsymbol{Aw-b})}{d\boldsymbol w} = 2\boldsymbol{A^T}(\boldsymbol{Aw-b}) = 0$$

求得

$$\boldsymbol{A^T}\boldsymbol{Aw} = \boldsymbol{A^Tb}$$

这玩意儿就是著名的 Normal Equation了。可以看到这是一个关于 w 的线性方程组，这个方程的每个解 w 就是对经验风险 $\hat R$ 的一个最小化。

接下来，学过线性代数的大概都知道，可以通过高斯消元来求解了，复杂度是$O(nd^2)$，也叫作OLS，即Ordinary Least Square，解得

$$\hat w = (A^TA)^{-1}A^Tb$$

D. ERM表现评估

回顾

回忆一下，我们首先定义了损失函数，即给定一个 x, y 对，$L(f(\boldsymbol{x}), y)$ 衡量了当输出为y的时候，使用预测函数预测 $f(\boldsymbol{x})$的损失是多少，在回归问题中，我们常常使用的损失函数是平方差损失，即 $L(f(\boldsymbol{x}), y) = (f(\boldsymbol{x}) - y)^2$。

紧接着，我们定义了风险函数，一个预测函数的（真实）风险为：

$$R(f) = \mathbb{E}_p[(f(\boldsymbol{X})-Y)^2] = \int\int p(\boldsymbol{x}, y)L(f(\boldsymbol{x}), y) d\boldsymbol{x} dy$$

其中p是x, y的分布，即产生数据的原分布。这里的风险衡量的是在期望的意义上，使用预测函数$f$来预测的风险有多大。我们的目标就是找到一个最小化风险的预测函数，我们在函数 $f$ 加个星号*上标，代表这是最优的参数，即：

$$f^* = \arg \min_f R(f)$$

但是，因为我们其实并不知道原分布是啥。退而求其次，我们利用插入原则，采用经验分布来替代原分布，然后通过最小化经验风险，来求解模型参数。这里的经验分布可以简单地理解为给n个训练数据每个数据点赋予 1/n 概率的一个新的分布。那么，根据定义我们可以得到：

$$\hat R(f) = \mathbb{E}_{ep}[(f(\boldsymbol{X})-Y)^2] = \frac{1}{n}\sum_{i=1}^n(f(\boldsymbol{x}_i)-y_i)^2$$

这样，我们通过ERM，得到预测函数：

$$\hat f = \arg \min_f \hat R(f)$$

评估

在线性回归中 $f(\boldsymbol{x}) = \boldsymbol{x}^T w$，所以这里用 $w$ 来区分不同的预测函数。首先先区分下几个量

• 真实风险 $R$
• 经验风险 $\hat R $，是个取决于训练数据的随机变量
• $\hat w$ 是让经验风险 $ \hat R $ 最小的解，也是个取决于训练数据的随机变量
• $w^*$ 是让真实风险 R 最小的最优解

ERM的真实风险 vs 最优解的真实风险

首先人们最关心的肯定就是 $\hat w$ 和 $w^$ 的真实风险差距了，因为说到底，我们想找的其实是 $w^$，但是没办法，只能找到一个近似值 $\hat w$，并且期待 $R(\hat w) \approx R(w^*)$。 事实上，我们可以证明，当 $n\rightarrow \infin$时，有

$$R(\hat w) \rightarrow R(w^*) + \frac{tr(cov(\epsilon W))}{n}$$

其中 $W = \mathbb{E}[XX^T]^{-1/2}，\epsilon = Y-X^Tw^*$ 。

证明过长，此处便不扩展，只以线性回归模型 $Y|X=x \sim N(x^T w, \sigma^2)$ 为例子，那么上边这个定理的结果可以简化为：

$$R(\hat w) \rightarrow R(w^*) + \frac{\sigma^2d}{n} = (1+\frac{d}{n})\sigma^2$$

ERM的经验风险 vs 真实风险

那么ERM的解 $\hat w$ 的风险和最优解 $w^*$ 的风险又有什么关系呢？因为前者是个随机变量，我们尝试比较它们的期望值，即 $\mathbb{E}[\hat R(\hat w)]$ 和 $ \mathbb{E}[R(\hat w)]$ 之间的关系。

直觉上，$\hat w$ 就是在训练数据上求得的最小化经验风险（即在训练数据上的风险）的解，那么其在原分布上的真实风险应该是更大的，这就像是测试数据的loss一般总比训练数据上的loss大一样。

实际上确实 $\mathbb{E}[\hat R(\hat w)] \le \mathbb{E}[R(\hat w)]$ ，借助最优解 $w^*$ 作为桥梁，证明起来也不复杂。

先尝试重新阐述下问题，如果 $\left(\boldsymbol{x}_{1}, y_{1}\right), \ldots,\left(\boldsymbol{x}_{n}, y_{n}\right), \left(\boldsymbol{x}, y\right) \in \mathbb{R}^{d} \times \mathbb{R}$ 是从某个概率分布 P 上采集的 独立同分布 随机数据点，为了方面描述，以下的风险都是针对平方损失而言，那么我们有：

对于最优解 $w^*$，我们有：

$$\begin{aligned}\mathbb{E}[\hat R(w^*)] &= \mathbb{E}[\frac{1}{n}\sum_{i=1}^n(\boldsymbol{x}^T_i w^* - y_i)^2]\\&=\frac{1}{n}\sum_{i=1}^n\mathbb{E}[(\boldsymbol{x}^T_i w^* - y_i)^2]\\&=\frac{1}{n}\sum_{i=1}^n\mathbb{E}[(\boldsymbol{x}^T w^* - y)^2] \\&= \frac{1}{n}\sum_{i=1}^nR(w^*) \\&= R(w^*)\end{aligned}$$

注意到第三行可以将 $\boldsymbol{x}^T_i, y_i$ 替换成 $\boldsymbol{x}^T, y$ 是因为它们是独立同分布的。

然后，因为 $\hat w = \arg \min_w \hat R(w)$ 以及 $w^ = \arg \min_w R(w)$，我们有 $\hat R(\hat w)\le \hat R(w^)$ 和 $R(w^*)\le R(\hat w)$，连立起来就是

$$\mathbb{E}[\hat R(\hat w)] \le \mathbb{E}[\hat R(w)] = R(w) \le \mathbb{E}[R(\hat w)]$$

过拟合 Overfitting

啥是过拟合？在上一小节中，我们证明了EMR的解的经验风险是小于等于真实风险的，当这个经验风险远小于真实风险的时候，我们称之为过拟合。

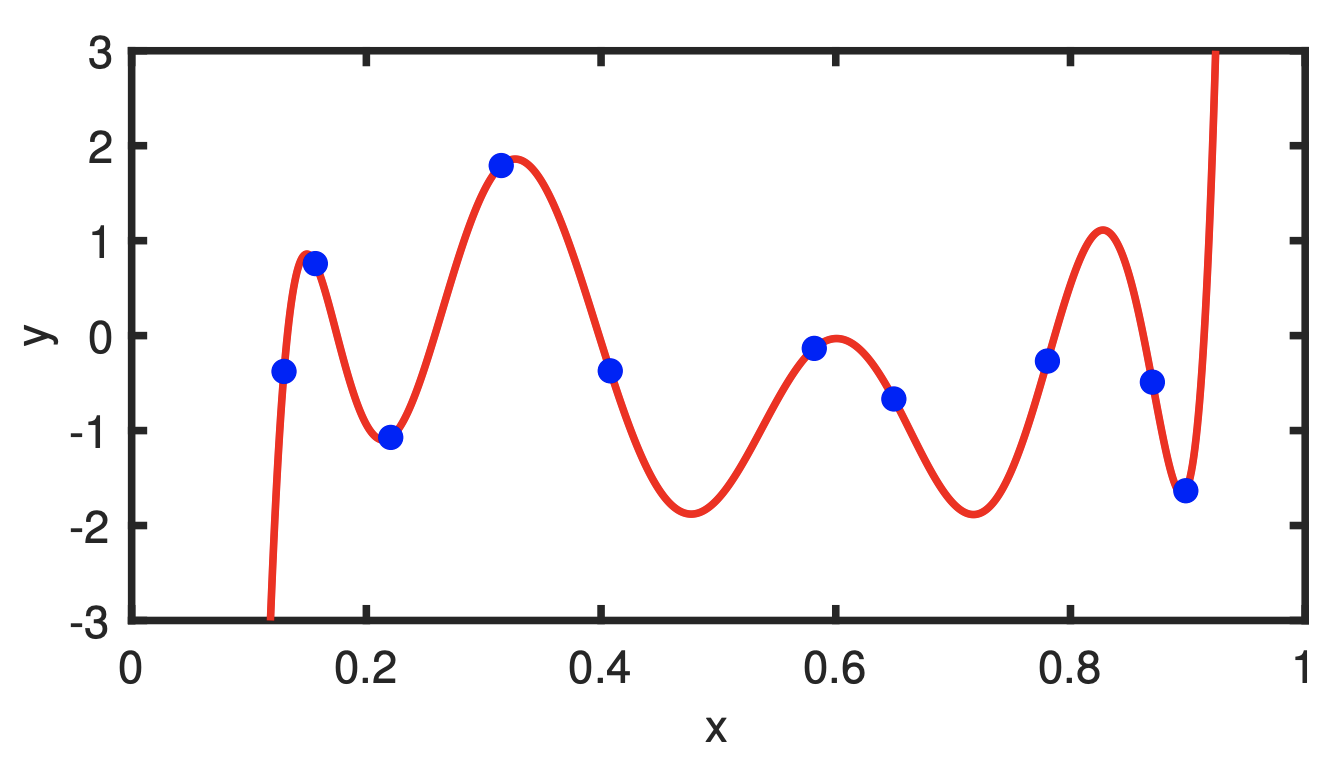
举个栗子，一般我们称一个特征变换 $\varphi(x) = (1, x, x^2,…,x^k)$ 作为一个 k 度的多项式展开，注意到变换后的特征维度是 k+1 维，一般来说，如果你的数据点个数小于等于 k+1 的话，都可以用它来完美拟合，即找到一个ERM的解使得经验风险为零，即 $\hat R(\hat w) = 0$，即便是真实风险远大于零，即 $R(\hat w) \gg 0$。