Zejun Lin's Blog

异国漂泊，野蛮生长

0%

Easy and Almost-Bug-Free Way to Solve Parsing Problems on Leetcode

Posted on Edited on In

What it solves for

Parsing problems on leetcode are usually hard to write, hard to debug and variable for different situations, which makes it time-consuming. Sample problems might be the series of calculators. If you are trying to find a general, easy way (almost no annoying bugs after you finish it too!) to solve this kind of problems, then you should read this.

Basically this post introduce simple BNF and a easy-to-write Recursive Descent Parsing template to implement BNF.

Backus-Naur Form (BNF) Grammar

Wiki defines BNF as a notation technique for context-free grammars, often used to describe the syntax of languages such as computer programming languages. Please don’t be deterred by this abstract concept. It will be quite clear and simple after walking through an example. (If you have taken compiler class before, you can skip this chapter…)

A basic example might be Basic Calculator II, which asks to write a calculator for expression only with +, -, *, / and positive numbers. The BNF that describes the syntax of such an expression looks like this:

1
2
3
4
<Expr> ::= <Term> {(+|-) <Term>}
<Term> ::= <Number> {(*|/) <Number>}
<Number> ::= <Digit>{<Digit>}
<Digit> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9

Let me explain the symbols used here. Usually a BNF is consisted of the following:

  • Non-terminals: names enclosed in <, > like <Number>, which can generate a kind of expression — usually consisting of different terminals and non-terminal
  • Terminals: characters like +, -, *, /, 1, 2, …, which cannot generate into another expression.
  • ::=: Just like an assignment, interpreted as “is defined as“. It describes that the left-hand-side Non-terminals will generate an expression in the right-hand-side. For each statement like this, we call it a production.
  • |: A Non-terminals might generate into different expressions, you can use | to separate them, which means OR. Note that it has the lowest priority, so if you want to expression an or between two small items, use () to group them.
  • {}: Items existing 0 or more times are enclosed in curly brackets
  • []: Optional items enclosed in square brackets

So how is this BNF related to the calculator I described above?

Well, you can use this BNF, specifically, the <Expr> non-terminal to generate all legal expressions of this calculator. Let me explain each production below:

  • <Expr> ::= <Term> {(+|-) <Term>}: An <Expr> might be one or multiple <Term> concatenated by + or -.
  • <Term> ::= <Number> {(*|/) <Number>}: Similarly, each <Term> is either a <Number> or muliple <Numbere> concatenated by * or /.
    • Note that we distinguish <Expr> and <Term> because the priority of * and / is higher than + and -, which helps to calculate correctly.
  • <Number> ::= <Digit>{<Digit>}: a <Number> is consisting of one or more <Digit>.
  • <Digit> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9: this one is obviouse, a <Digit> is just a digit.

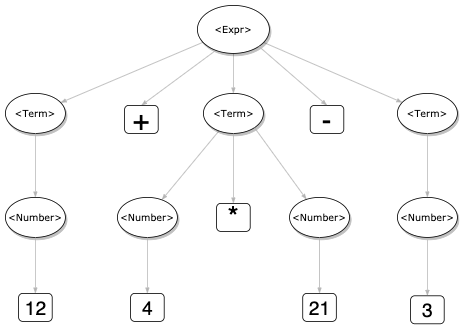
An example — 12 + 4 * 21 - 3​ can be described as the BNF tree below:

BNF_tree

Converting BNF to C++ code — Recursive Descent Parsing

There are many ways to implement a BNF parser depending on the complexity of the grammar. Usually for problems on leetcode, a simplest Predictive Recursive Descent Parser. Note that it is only possible for the class of LL(k) grammars. Here, LL(k) means you can decide which production to use by examining only the next k tokens of input. Usually a LL(1) will be enough.

For example, you want to parse a term using <Term> ::= <Number> | (<Expr>). You can look ahead the next token (LL(1)) to decide whether this <Term> is intepreted as a <Number> or an <Expr>

  • if the next token is a digit like 1, 2, then you know it’s a <Number>;
  • if the next token is a left parenthesis (, then you know it’s a <Expr>;
  • Otherwise you should raise an error…

Still, take the Basic Calculator II as an example. The Algorithm is very simple, consisting of the following parts/steps:

  • A global variable of type string —input— stores the input and another global variable stores the current index —idx— of the input.
  • A lookahead function reads the next token but NOT increment idx.
  • A getchar function reads the next token AND increment idx.
  • Write a function for each Non-terminal , which determines which production to use, consume the input string and calculate the result.
    • For {} symbols, remember it means that items inside exists 0 or more times.
      • We use a while loop — fisrt use lookahead to check whether the next token is the beginning of the item inside [].
      • If it is, we recursively call the corresponding function.
    • For [] symbols, just use an if statement to check.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class Solution {
/* BNF
<Expr> ::= <Term> {(+|-) <Term>}
<Term> ::= <Number> {(*|/) <Number>}
<Number> ::= <Digit>{<Digit>}
<Digit> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
*/
private:
    string input;
    int idx;
    char lookahead(){
        while (input[idx] == ' ') ++idx;
        return input[idx];
    }
    char getchar(){
        return input[idx++];
    }
    long expr(){
        long res = term();
        while (lookahead() == '+' || lookahead() == '-'){
            if (getchar() == '+') res += term();
            else res -= term();
        }
        return res;
    }
    long term(){
        long res = number();
        while (lookahead() == '*' || lookahead() == '/'){
            if (getchar() == '*') res *= number();
            else res /= number();
        }
        return res;
    }
    long number(){
        long res = 0;
        while (lookahead()>='0' and lookahead()<='9'){
            res = res * 10 + (getchar()-'0');
        }
        return res;
    }
public:
    int calculate(string s) {
        input = s;
        return expr();
    }
};

More examples and solution code using BNF

The following are all problems on Leetcode. I will provide the BNF and my code.

Ternary Expression Parser

If you want to practice the algorithm above, you would better try this simple one first.

The problem is described as:

Given a string representing arbitrarily nested ternary expressions, calculate the result of the expression. You can always assume that the given expression is valid and only consists of digits 0-9, ?, :, T and F (T and F represent True and False respectively).

Example inputs and outputs:

  • Example 1:
1
2
3
Input: "T?2:3"
Output: "2"
Explanation: If true, then result is 2; otherwise result is 3.
  • Example 2:
1
2
3
4
5
6
Input: "T?T?F:5:3"
Output: "F"
Explanation: The conditional expressions group right-to-left. Using parenthesis, it is read/evaluated as:
             "(T ? (T ? F : 5) : 3)"                   "(T ? (T ? F : 5) : 3)"
          -> "(T ? F : 3)"                 or       -> "(T ? F : 5)"
          -> "F"                                    -> "F"
  • Solution:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
/*
BNF:
Expr ::= Digit | Ternary
Ternary ::= [F|T] ? Expr : Expr
*/
private:
    string input;
    int idx = 0;
    char lookahead(int offset = 0){
        return input[idx+offset];
    }
    char getchar(){
        return input[idx++];
    }
    char expr(){
        if (lookahead(1) == '?') return ternary();
        else return digit();
    }
    char ternary(){
        char cond = getchar();
        getchar(); // discard `?`
        char res[2];
        res[0] = expr();
        getchar(); //discard `:`
        res[1] = expr();
        return res[cond != 'T'];
    }
    char digit(){
        return getchar();
    }
public:
    string parseTernary(string expression) {
        input = expression;
        return string(1, expr());
    }
};

Basic Calculator III

A calculator with +-*/ and ().

  • Very similar to the example in the tutorial, except that there is ().
    • Remember in the previous example, Term is interpreted as different Number? Now it can also be another Expr with () — I call it Factor, which is either a Number or an Expr.
  • Actually I extend it so that it can solve negative number as well ! — Note the optional +/- at the begining of Expr and Factor

  • Since that are () in the input string (also a keyword of BNF), I use \( to mean that it is a true ( charater in the input string.

  • Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
class Solution {
/* BNF
Expr ::= [+|-] <Term> { +|- <Term>}
Term ::= Factor { (* | / ) <Factor>}
Factor ::= {-} ( Number | ( \( Expr \) )
Number ::= Digit{Digit}
*/
private:
    string input;
    int idx;
    char lookahead(){
        while (input[idx] == ' ') ++idx;
        return input[idx];
    }
    char getchar(){
        return input[idx++];
    }
    long expr(){
        long res = 0;
        if (lookahead() != '+' && lookahead() != '-'){
            res += term();
        }
        while (lookahead() == '+' || lookahead() == '-'){
            if (getchar() == '+') res += term();
            else res -= term();
        }
        return res;
    }
    long term(){
        long res = factor();
        while (lookahead() == '*' || lookahead() == '/'){
            if (getchar() == '*') res *= factor();
            else res /= factor();
        }
        return res;
    }
    long factor(){
        long res = 1;
        if (lookahead() == '-'){
            res = -1;
            getchar();
        }
        if (lookahead() == '('){
            getchar();
            res *= expr();
            getchar(); // discard ) symbol
        }
        else if (lookahead()>='0' && lookahead()<='9')
            res *= number();
        return res;
    }
    long number(){
        long res = 0;
        while (lookahead()>='0' and lookahead()<='9'){
            res = res * 10 + (getchar()-'0');
        }
        return res;
    }
public:
    int calculate(string s) {
        input = s;
        return expr();
    }
};

Parse Lisp Expression

Here comes a much harder one. Details of problem description please refer to leetcode.

There are several important points to note:

  • In the previous example, every token is just a single character. It doesn’t work for most grammar.
    • For example, without seeing the whole word, you will not a token starting with w is just a variable name or the keyword while in a programming language like c++.
    • But this won’t make things complicated. You just need to write a function to split input string into an array of tokens according to delimiter like space — usually including keywords in that grammar too.
  • LL(1) is not sufficient here, LL(2) is needed. But this is also a easy thing. You just need to provide an offset parameter in the lookahead function so that you can “LOOK INTO” the next next token.
    • Example might be Expr ::= Let | Addmult | Term.
    • Say the input string is (add 1 2) — ["(", "add", "1", "2", ")"] as tokens — you will not know it should be intepreted into a Addmult or a Let if you just know the next token is (.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
class Solution {
/* Try BNF
Expr ::= Let | Addmult | Term 
Let ::= \( {Var Expr} Expr \)
Addmult ::= \( (add|mult) Expr Expr \)
Term ::= ([-] Number) | Var
Number ::= digit {digit}
Var :: char {char|digit}

But for let statement:
Cuz Expr => Var, you cannot decide whether there's another {Var Expr} or not without LL(2)
But if next == '(', then it's definitely expr()
*/
private:
    vector<string> tokens;
    int idx = 0;
    map<string, vector<int>> variables;
  	/********* Helper Functions **************/
    vector<string> split(const string& str, set<char> delimiters){
        vector<string> tokens;
        string token = "";
        for(char c: str){
            if (delimiters.find(c) != delimiters.end()){
                if (token != "") tokens.push_back(token);
                if (c != ' ' && c != '\0') tokens.push_back(string(1, c));
                token = "";
            }
            else token += c;
        }
        if (token != "") tokens.push_back(token);
        //for_each(tokens.begin(),tokens.end(),[](string& t){cout<<t<<endl;});
        return tokens;
    }
    string lookahead(int offset=0){
        return tokens[idx+offset];
    }
    string gettoken(){
        //cout<<tokens[idx]<<endl;
        return tokens[idx++];
    }
    inline bool isnumber(const string& s){ return (s[0] >= '0' && s[0] <= '9') || s[0] == '-';}

  	/********* Parsing Functions **************/
    int expr(){
        int res = 0;
        if (lookahead() == "(") {
            if (lookahead(1) == "let") res = let();
            else if (lookahead(1) == "add" || lookahead(1) == "mult") res = addmult();
            else throw "Error";
        }
        else{
            res = term();
        }
        return res;
    }
    int let(){
        gettoken(), gettoken(); //discard `(`, `let`
        int res = 0;
        string token;
        vector<string> var_name;
        while (true){
            token = lookahead();
            if (token[0] == '('){ // must be a expression
                res = expr();
                break;
            }
            if (isnumber(token)){ // a number
                cout<<"---"<<token<<endl;
                res = stoi(token);
                break;
            }
            // then it should be a variable -- token
            token = gettoken();
            if (lookahead()[0] == ')'){
                res = variables[token].back();
                break;
            }
            else{
                var_name.push_back(token);
                variables[token].push_back(expr());
            }
        }
        gettoken(); // discard )
        for (string& var: var_name){
            variables[var].pop_back();
        }
        return res;
    }
    int addmult(){
        gettoken(); // discard (
        string op = gettoken();
        int operand1 = expr(), operand2 = expr();
        gettoken(); //discard ')'
        return op=="add"?operand1+operand2:operand1*operand2;
    }
    int term(){
        int res = 0;
        if (isnumber(lookahead())){
            res = number();
        }
        else res = var();
        return res;
    }
    int number(){
        return stoi(gettoken());
    }
    int var(){
        return variables[gettoken()].back();
    }
public:
    int evaluate(string expression) {
        tokens = split(expression, set<char>{'(', ')', ' '});
        return expr();
    }
};

Basic Calculator IV

  • The hardest one!
  • No new contents. You should be able to figure it ourt if you have finished the previous example…
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
class Solution {
/* BNF
Expr ::= [+/-] <Term> {+|- <Term>}
Term ::= Factor {* <Factor>}
Factor ::= {-} ( Var | Number | ( \( Expr \) )

Result stored as unordered_map:
    - string -> coff
    - value -> value as coff
*/
private:
    vector<string> tokens;
    int idx = 0;
    unordered_map<string, int> variables;
    /* Helper Functions */
    vector<string> split(const string& str, set<char> delimiters, bool withdel=true){
        vector<string> tokens;
        string token = "";
        for(char c: str){
            if (delimiters.find(c) != delimiters.end()){
                if (token != "") tokens.push_back(token);
                if (c != ' ' && c != '\0' && withdel) tokens.push_back(string(1, c));
                token = "";
            }
            else token += c;
        }
        if (token != "") tokens.push_back(token);
        //for_each(tokens.begin(),tokens.end(),[](string& t){cout<<t<<endl;});
        return tokens;
    }
    void split_and_sort(string& s){
        vector<string> vars = split(s, set<char>{'*'}, false);
        sort(vars.begin(), vars.end());
        s = vars[0];
        for (int i = 1; i < vars.size(); ++i) s += "*" + vars[i];
    }
    unordered_map<string, int> multiply(const unordered_map<string, int>& a, const unordered_map<string, int>& b){
        unordered_map<string, int> res;
        for (auto& i: a){
            for (auto& j: b){
                string term = i.first + "*" + j.first;
                if (term == "*"){ // both are number
                    res[""] += i.second * j.second;
                } else{ // have variables
                    split_and_sort(term);
                    res[term] += i.second * j.second;
                }
            }
        }
        return res;
    }

    /* Parsing Functions */
    string lookahead(int offset=0){
        return tokens[idx+offset];
    }

    string gettoken(){
        //cout<<tokens[idx]<<endl;
        return tokens[idx++];
    }
    inline bool isdigit(char c){ return c >= '0' && c <= '9';}
    
    unordered_map<string, int> expr(){
        unordered_map<string, int> res;
        int sign = 1;
        if (lookahead()[0] != '+' && lookahead()[0] != '-')
            res = term();

        while (lookahead()[0] == '+' || lookahead()[0] == '-'){
            sign = gettoken()[0]=='+'?1:-1;
            for (auto&& k: term()){
                res[k.first] += sign * k.second;
            }
        }
        return res;
    }
    unordered_map<string, int> term(){
        unordered_map<string, int> res = factor();
        while (lookahead()[0] == '*'){
            gettoken(); // discard *
            res = multiply(res, factor());
        }
        return res;
    }
    unordered_map<string, int> factor(){
        unordered_map<string, int> res;
        int sign = 1;
        string token = gettoken();
        if (token[0] == '-'){
            sign = -1;
            token = gettoken();
        }
        if (token[0] == '('){
            res = expr();
            for (auto& t: res) t.second = sign * t.second;
            gettoken(); // discard ) symbol
        }
        else if (isdigit(token[0])) // a number
            res[""] = sign * stoi(token);
        else{ // a variable
            if (variables.find(token) != variables.end())
                res[""] = sign * variables[token];
            else res[token] = sign;
        }
        return res;
    }
    void store_variables(const vector<string>& evalvars, const vector<int>& evalints){
        for (int i = 0; i < evalvars.size(); ++i)
            variables[evalvars[i]] += evalints[i];
    }
    static inline bool cmp(const string& a, const string& b){
        int da = count(a.begin(), a.end(), '*');
        int db = count(b.begin(), b.end(), '*');
        if (da != db) return da > db;
        return a < b;
    }
public:
    vector<string> basicCalculatorIV(string expression, vector<string>& evalvars, vector<int>& evalints) {
        store_variables(evalvars, evalints);
        tokens = split(expression, set<char>{'-', '+', '*', '(', ')', ' ', '\0'});
        tokens.push_back("$"); // guard for end of input
        auto res = expr();

        vector<string> ans;
        vector<string> keys;

        // sort keys according to term degree and alphabet
        for (auto& k: res) keys.push_back(k.first);
        sort(keys.begin(), keys.end(), cmp);

        string value = ""; // store numeric value if there is any
        for (auto& k: keys){
            if (res[k] == 0) continue;
            if (k == "") value = to_string(res[""]);
            else ans.push_back(to_string(res[k]) + "*" + k);
        }
        if (value != "") ans.push_back(value);
        return ans;
    }
};