Leetcode Weekly

Leetcode每周碎碎念——参加了一个训练计划，每周输出一个Leetcode题目，除了有特别想总结的专题，通常会把内容都倒到这里。

Smallest Common Region

一个单次询问的 LCA (Lowest Common Ancestor) 问题， 题目给出一堆Regions，给出Region之间的包含关系，然后求一个最小的包含两个Regions A, B的一个Region。可以看出这是一棵树，求的是节点 A, B的最低祖先。

题目输入样例是一堆 List, 比如 ["Earth","North America","South America"] 代表 Earth 包含后面所有的，当然它也包含它本身。

这里有个常用的技巧是 dfs 的出入时间，即你运行一个dfs，每次转移时间 t 就加一，那么对于每个点 （假设为 i），都有个进入的时间 tin[i] 和出去的时间 tout[i]，不难得出，如果点 i 为 j 的祖先，那么 j 的 tin 和 tout必然被包含在 i 的 tin 和 tout 中。

因为这周有点赶时间，下面贴出有点丑的代码和注释。

class Solution:
    def findSmallestRegion(self, regions: List[List[str]], region1: str, region2: str) -> str:
        graph = {line[0]:line[1:] for line in regions}
        regions = set() # 存所有节点
        for line in graph.values():
            regions |= set(line)
        nodes = set(regions) # 此时 node 为有入度的点
        regions |= set(graph.keys())
        roots = regions - nodes # 减去后即是没有入度的点，即为这片森林的树根们

        tinout = {} # 我们用字典来存出入时间，{node_id: (tin, tout)}
        def dfs(region, t):
            """return the lastest used time t"""
            if region not in tinout:
                tinout[region] = [t, -1]
            for child in graph.get(region, []):
                t = dfs(child, t+1)
            t += 1
            tinout[region][1] = t
            return t
        t = -1
        for region in roots: # 对于所有树根都dfs一下
            t = dfs(region, t+1)

        def is_ancestor(f, c):
            return tinout[f][0] <= tinout[c][0] and tinout[c][1] <= tinout[f][1]
        ans = None
        for region in regions:
            if is_ancestor(region, region1) and is_ancestor(region, region2):
                if ans is None or is_ancestor(ans, region):
                    ans = region
        return ans

Minesweeper

• Wikipedia)

• online game

扫雷，游戏规则想必都很熟悉，这个题目就是模拟下用户点击某个位置后，系统给出的结果。

简单地说下游戏规则

• 点开的格子里
  • 是数字的，代表这个各自周围的八个格子中有多少个雷
  • 空格代表没雷
• 没点开的格子
  • 可能是雷，数字或空格

玩家点开一个没点开的格子

• 如果是雷，游戏结束
• 如果那个格子周围有雷，那么格子翻开显示一个数字代表周围有几个雷
• 如果那个格子是个空格，那么系统自动帮玩家开这个格子周围的所有格，以此递归

这道题本身没有什么意思，就简单地按照规则bfs一下就好了，给出随手写的代码如下

def updateBoard(self, board: List[List[str]], click: List[int]) -> List[List[str]]:
    visited = {tuple(click)}
    n, m = len(board), len(board[0])
    click = [click]
    while click:
        nclick = []
        for i, j in click:
            if board[i][j] == 'M':
                board[i][j] = 'X'
            elif board[i][j] == 'E':
                tmp, n_mines = [], 0
                for di in range(-1, 2):
                    for dj in range(-1, 2):
                        if di == dj == 0:
                            continue
                        ni, nj = i + di, j + dj
                        if not (0 <= ni < n and 0 <= nj <m) or (ni, nj) in visited:
                            continue
                        tmp.append((ni, nj))
                        if board[ni][nj] == 'M':
                            n_mines += 1
                if not n_mines:
                    nclick += tmp
                    visited |= set(tmp)
                    board[i][j] = 'B'
                else:
                    board[i][j] = str(n_mines)
        click = nclick
    return board

但我做了这题之后，得益于题目的游戏链接，不可自拔地玩了一周的扫雷。。。

闲起来就点点，还是蛮有意思的，有种比赛打题目的感觉，medium从一开始的一百左右玩到了五十多。

Median of Two Sorted Arrays

题目描述

题意为给两个sorted array，找出他们的中位数。

比如

• A = [1, 3]， B = [2]，则median = 2
• A = [1, 2]， B = [3, 4]，则median = (2 + 3) / 2 = 2.5

解法

假设两个数组长度分别为n, m，一个Trivial的解法可能是讲两个数组merge起来，然后找中间的那个，复杂度是O(n + m)。当然，题目本意是要个 log (n+m) 级别的算法。其实这个题目并不难，“排好序” + “log级别”，很明显就是用二分来做， 只是没有清晰思路的话很容易被各种corner case绕晕。

我从这个题目中学到的就是要对每样东西都有 清晰的定义， 比如中位数， 比如写代码时候的每一个变量

在统计学上，中位数 用于将 一个数字集合 分成长度相等的两个子集，且其中一个集合的任意数字 大于 另外一个集合的所有数字。

• 那么，对于偶数长度的集合，假设分为 left 和 right 两个集合且 left < right，则 median = $\frac{\max(left) + \min(right)}{2}$
• 对于奇数长度的，median为将left 和 right分开的最中间的那个元素。

清楚了中位数的定义之后，就知道其实我们只要分别把A, B分成两部分，假设为 leftA, rightA, leftB, rightB，且满足两个条件

1. 左右长度相等：len(leftA) + len(leftB) == len(rightA) + len(rightB) == (len(A) + len(B)) // 2
2. 左边的任意元素小于右边：已知排好序，所以 leftA < rightA 且 leftB < rightB，所以只要保证 leftA < rightB 且 leftB < rightA 就行了

这里可以看出，假设我们知道A怎么分，比如leftA最后一个元素的index是i，那么根据1就可以算出B是怎么分的（假设leftB最后一个元素index是j），然后就能 O(1) check下是否满足 2。容易知道，我们可以用二分来找到 A 的分法，即index i。

这里引入另外一个可能出bug的地方，就是必须明确二分的值的定义和可能的值域。在下面这里，我给出二分值 i 的定义，i 作为 leftA的最后一个元素下一个index， 即，leftA index范围为左闭右开区间 [0, i)，可供选择的 i 的范围就是 [0, len(A)]，其中，最短为 i == 0，leftA为 [0, 0)，即为空；最长为 i == len(A)，leftA为[0, len(A))，即为A的全部。以下讨论下三种情况

• 假设 leftA, leftB, rightA, rightB都不为空，且max(leftA) = l1, max(leftB) = l2, min(rightA) = r1, min(rightB) = r2
  • 已知排好序（所以l1 < r1 && l2 < r2），所以只需要check l1 < r2 && l2 < r1，如果符合，那就是正确分好四个部分，可以返回median了
  • 如果 l1 > r2，即 leftA 最大元素有比 rightB大的，那么说明A上分割点 i 还应该左移，让 l1 = max(leftA) 更小一点， 所以缩小二分区间为 [l, mid)
  • 否则，可知 l2 > r1，那么相反地，i 右移，即[mid+1, r)
• 若 leftA为空，那就是不用check l1 < r2了，我们把 l1 置 为 负无穷，让 l1 < r2 永远满足
• 若 rightA为空，则无需check l2 < r1，那么把r1 置为 正无穷， 让 l2 < r1 永远满足
• 对leftB, rightB为空的情况同理。

当我们分好两个部分之后，如果长度为奇数个，因为我们在计算一半长度half时候为向下取整，即比如有5个，那么 5 // 2 = 2，即len(leftA) + len(leftB) == 2，所以median是 min(r1, r2）（右边比较小的那个）

若长度为偶数个，那么就是left较大的(max(l1, l2))，和right 较小的 (min(r1, r2))的平均数。

附上python 代码如下

class Solution:
    def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
        if len(nums1) > len(nums2):
            nums1, nums2 = nums2, nums1
        n1, n2 = len(nums1), len(nums2)
        half = (n1 + n2) // 2 # how many elements in the left including pivot points
        l, r = 0, n1 + 1
        # means pick [0, l) from nums1
        # so if l == 0, [0, 0) means pick none
        # if l == n1, [0, n1) means pick all
        while l < r:
            mid = (l + r) // 2
            idx = half - mid
            l1 = nums1[mid-1] if mid != 0 else -float('inf')
            l2 = nums2[idx-1] if idx > 0 else -float('inf')
            r1 = nums1[mid] if mid < n1 else float('inf')
            r2 = nums2[idx] if idx != n2 else float('inf')
            # print(l, r, mid, '--', l1, l2, r1, r2)
            if l1 <= r2 and l2 <= r1:
                if (n1 + n2) & 1:
                    return min(r1, r2)
                return (max(l1, l2) + min(r1, r2)) / 2
            elif l1 > r2:
                r = mid
            else:
                l = mid + 1

String to Integer (atoi)

一个水题，说是让把一个string转化成一个int，按照题目要求把每种情况都 if 下就行了，要求有以下几点

• 数字左右两边可能有空格，后边可能有其它字符比如字母，都需要忽略
• 数字可能带正负号
• 如果string的开端不是正负号或者数字，那么它就不能被转化，则应该返回 0
• 注意你是在一个只能处理int的机器上，所以返回的数字需要在区间 [$−2^{31}, 2^{31} − 1$]里面

需要注意的是，最后一点规定了题目只能使用 32位int，所以要有判断是否overflow的逻辑，而不能直接用long，贴几个可能的样例输入，以及corner cases:

Input	“ -42”	“4193 with words”	“words and 987”	“-91283472332”	2147483649	+-2
Ouput	42	4193	0	-2147483648	2147483647	0

下面贴上 c++ 代码

class Solution {
public:
    int myAtoi(string str) {
        int sign = 1;
        reverse(str.begin(), str.end());
        while (!str.empty() && str.back() == ' ') str.pop_back();
        if (str.empty()) return 0;
        if (str.back() == '-') sign = -1;
        if (str.back() == '+' || str.back() == '-') str.pop_back();
        if (str.empty() || str.back() < '0' || str.back() > '9') return 0;
        int ans = 0;
        if (sign == 1){
            while (!str.empty()){
                if (str.back() < '0' || str.back() > '9') break;
                if (ans > INT_MAX / 10.0 || (INT_MAX - ans*10) < str.back() - '0') return INT_MAX;
                ans = ans * 10 - '0' + str.back();
                str.pop_back();
            }
            return ans;
        }
        while (!str.empty()){
            if (str.back() < '0' || str.back() > '9') break;
            if (ans < INT_MIN / 10.0 || (ans*10 < INT_MIN + 100 && (ans*10 - INT_MIN) < str.back() - '0')) return INT_MIN;
            ans = ans * 10 + '0' - str.back();
            str.pop_back();
        }
        return ans;
    }
};

Gas Station

题目描述

你要旅行经过N个加油站，这N个加油站组成一个圈（环路）。给两个数组，一个是gas代表每个加油站各有多少单位的油，另一个是cost代表从某个加油站到它下一个加油站需要消费多少油。

要求如果你能从某个加油站出发绕N个加油站一圈的话，返回这个加油站的index，否则返回-1

例子：

输入：

gas = [1,2,3,4,5]
cost = [3,4,5,1,2]

输出：3

解释:
Start at station 3 (index 3) and fill up with 4 unit of gas. Your tank = 0 + 4 = 4
Travel to station 4. Your tank = 4 - 1 + 5 = 8
Travel to station 0. Your tank = 8 - 2 + 1 = 7
Travel to station 1. Your tank = 7 - 3 + 2 = 6
Travel to station 2. Your tank = 6 - 4 + 3 = 5
Travel to station 3. The cost is 5. Your gas is just enough to travel back to station 3.
Therefore, return 3 as the starting index.

解法

能肯定的一点是，如果所有的gas加起来没有cost多的话，那么肯定是不能绕一周的。那么反过来，如果gas的和不小于cost，是否能保证就有解呢？用题目中的例子画个图，发现确实是这样。

首先合并下两个数组，从 gas 减去 cost，那么新的数就代表从加油站 i 想去到 i+1，到达 i 的时候车上至少要有多少油，也可以理解为需要消耗多少油 （负为消耗，正为可以剩余）。

按照上边的说法，如果从第0个加油站出发，可以画出如下的图，横坐标代表加油站的index，纵坐标代表从第零个加油站到当前加油站 i ，一开始 需要多少油才能要到达下一个 i+1。比如在第0个的时候，需要 $gas[0] - cost[0] = 1 - 3 = -2$，在第1个的时候也需要 -2，但因为是从零出发的，原本已经需要-2了，所以在1的时候就累计需要-4了。

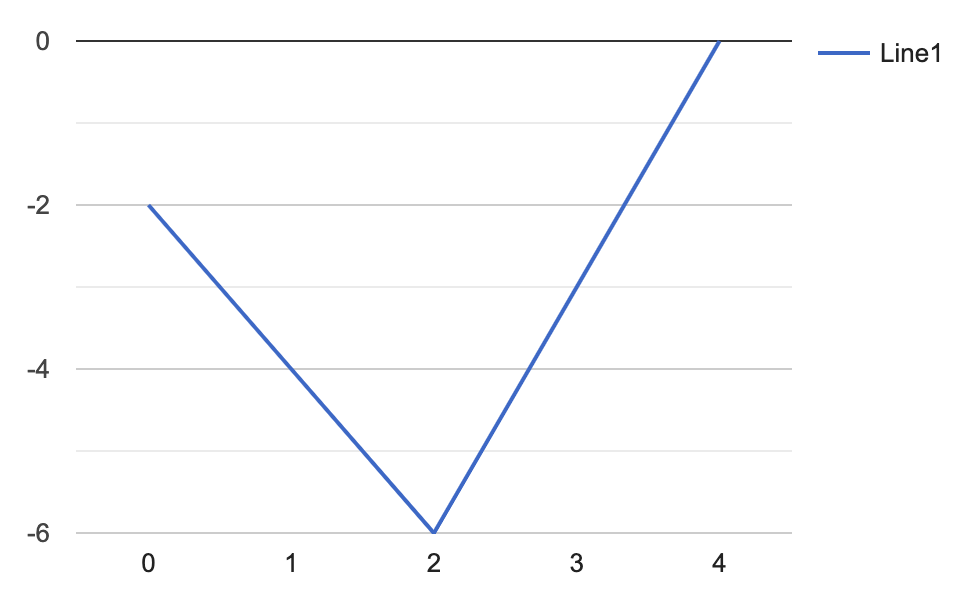
可以看到，在第二个加油站的时候需要的油最多，达到了-6，之后需要的油就不断减少了—即折线上升。因为总的油是够的，那如果从最低点开始（即第二个加油站），不就能把整个折线图往上推到直线 y = 0 上吗？

确实如此，因为你是从最低点开始的，那个时候是0，那么后面怎么折腾也不会再跌落到0。

假设从第二个加油站出发，可以得到一个新的图如下：

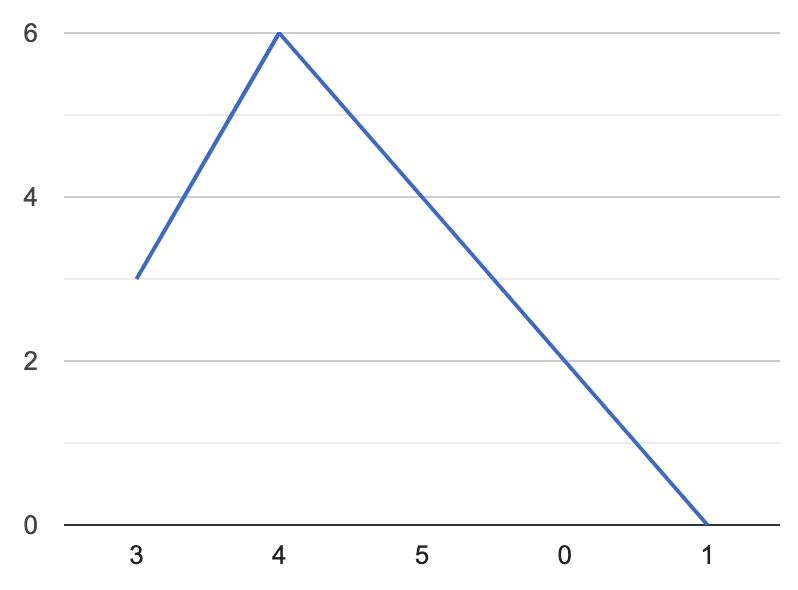
所以，这题其实只要先判断下总的油够不够，够的话就找到油最少的那个index i，返回 i+1就行了，可行的代码如下

class Solution:
    def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:
        if sum(gas) - sum(cost) < 0: return -1

        stock = idx = 0
        minimun = float('inf')
        for i, (g, c) in enumerate(zip(gas, cost)):
            stock += g - c
            if stock < minimun:
                minimun = stock
                idx = i + 1
        return idx % len(gas)

另外一种写法是，每次遇到存油小于0的（即从当前规定的起点不可行），就把开始的index设置为下一个，然后stock置为零，因为无论如何也有一个index是可行的，所以在这个index前面的不需要考虑。

class Solution:
    def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:
        if sum(gas) - sum(cost) < 0: return -1

        stock = idx = 0
        for i, (g, c) in enumerate(zip(gas, cost)):
            stock += g - c
            if stock < 0:
                stock = 0
                idx = i + 1
        return idx

Word Break I/II

题目描述

给一个字典wordDict里面有一些单词，然后再给一个字符串s，想让你

• Word Break I: 判断 s 是不是能够由 wordDict里面的词构成
  • Input: s = “leetcode”, wordDict = [“leet”, “code”]
  • Output: True
    • because “leetcode” can be separated into “leet” + “code”
• Word Break II: 找出所有可能的构成方式
  • Input: s = “catsanddog” wordDict = [“cat”, “cats”, “and”, “sand”, “dog”]
  • Output: [“cats and dog”, “cat sand dog”]
    • 有两种构成方式，用空格隔开

解法

这题是个经典的记忆化搜索题目，bottom up可以每次搜s[i:]，从后往前搜，用dp记录中间结果降低复杂度; Top down用递归同理。下面贴 Word Break II的代码，I同理

class Solution:
    def wordBreak(self, s: str, wordDict: List[str]) -> List[str]:
        wordDict = set(wordDict)
        @lru_cache(None)
        def dfs(begin):
            if begin >= len(s): return [""]
            res = []
            for end in range(begin+1, len(s)+1):
                if s[begin:end] in wordDict:
                    head = (" " if begin else "") + s[begin:end]
                    res.extend([head + item for item in dfs(end)])
            return res
        return dfs(0)

• 在写top down时，这里python有个很好用的修饰器是 lru_cache

• 它帮你记住当前参数的返回结果，下次函数被相同的参数调用时，会直接返回结果

• 其实也就是帮你自动化一个dp的过程，具体其它用法可以参考python文档

Candy Crush

题目描述

这题描述很简单，就是模拟完成糖果消消乐的消除过程 —

• 用一个面板来表示糖果网格的2D整数数组，不同的正整数board[i][j]表示不同类型的糖果，值board[i][j] = 0表示位置(i,j)处的单元格为空
• 如果三个或三个以上相同类型的糖果在垂直或水平方向相邻，则将它们同时“压碎”-这些位置将变为空。
• 在将所有糖果同时压碎后，如果板上的空白区域上方有糖果，则这些糖果将掉落，直到它们同时撞到糖果或底部。（没有新的糖果会掉到顶部边界之外。）
• 完成上述步骤后，可能会存在更多可以被压碎的糖果。如果是这样，则需要重复以上步骤。
• 如果不存在更多可以压碎的糖果（例如，板子稳定），则返回当前的板子。

例：

输入：
board = [[110,5,112,113,114]，[210,211,5,213,214]，[310,311,3,313,314]，[410,411,412,5,414]，[5,1,512,3,3]，[610,4,1,613,614]，[710,1,2,713,714] ，[810,1,2,1,1]，[1,1,2,2,2]，[4,1,4,4,1014]]

输出：
[[0,0,0,0,0]，[0,0,0,0,0]，[0,0,0,0,0]，[110,0,0,0,114]，[210， 0,0,0,214]，[310,0,0,113,314]，[410,0,0,213,414]，[610,211,112,313,614]，[710,311,412,613,714]，[810,411,512,713,1014]]

• 注意：
  • board长度将在[3，50]范围内。
  • board[i]长度将在[3，50]范围内。
  • 每个board[i][j]最初都将以[1，2000]范围内的整数开头。

解法

就是一道普通模拟题目，对于模拟题目推荐用python这种高度抽象的语言，好写。

先讲讲模拟的思路

1. 首先第一步肯定是消除，直接遍历，然后判断是否有三个格子都是相等的就行了，比如水平的话，若board[i][j] == board[i][j-1] == board[i][j-2]，那么这三个格子都需要消除。
   • 因为有水平和垂直两种消除，它们可能share同一个格子（考虑L形的一横一竖均为3个格子的情形），因为不能在水平或垂直扫到符合条件的时候就直接将格子置为零。
   • 注意到题目标明格子均为正数，那么我们可以将待消除的格子先变成相反数，然后处理完消除再进行一个把所有负数变成零的零化操作就行了。
   • 那么，条件判断就变成了abs(board[i][j]) == abs(board[i][j-1]) == abs(board[i][j-2])
2. 注意到横消除和竖直消除其实是一种操作，比如你只需要写个横消除，然后横消除后把矩阵顺时针旋转90度，再来个横消除，然后再逆时针旋转回来就行了。
   • 旋转在python里面是trivial的事情，只需要一行简单代码，比如逆时针旋转90度——先zip(*board)转置，然后在[::-1]颠倒就行了
3. 接下来是把空位（即0的格子）压满，同样只需要写个一个方向的拉，比如下文的pull_left，然后旋转跳跃…..
   • 压满就是用filter过滤下0，然后再在末端补齐下0保持每行的长度不变就行了。
4. 重复以上过程直到不能再消除。

以下贴出我的解法，主要有几个点需要注意

• 一是步骤比较多，推荐模块化，把每个功能抽象成一个函数，即可以增加代码可读性；又方便写完一个函数后即时unit-test该模块的功能是否完整，减少debug难度；还方便代码重复利用。
• 二是……好像也没啥了……

class Solution:
    def candyCrush(self, board: List[List[int]]) -> List[List[int]]:
        if not board or not board[0]:
            return board
        def eliminate(board) -> bool:
            # 水平方向的消除，返回是否有做任意消除
            modified = False
            for i in range(len(board)):
                for j in range(2, len(board[i])):
                    if board[i][j] and
                        abs(board[i][j-2]) == abs(board[i][j-1])
                                            == abs(board[i][j]):
                        board[i][j-2] = board[i][j-1] =
                        board[i][j] = -abs(board[i][j])
                        modified = True
            return modified

        def zeroize(board):
            # 把负数标记给弄成0
            return [[max(i, 0) for i in line] for line in board]

        def rotate(board, clockwise = True):
            # 旋转矩阵
            Tboard = map(list,zip(*board))
            if clockwise:
                return [line[::-1] for line in Tboard]
            else:
                return list(Tboard)[::-1]

        def pullleft(board):
            # 把零视为空格子，往左压
            n_col = len(board[0])
            board = [list(filter(lambda x:x, line)) for line in board]
            board = [line+[0]*(n_col-len(line)) for line in board]
            return board

        modified = True
        while modified:
            modified = False
            modified |= eliminate(board)
            board = rotate(board)
            modified |= eliminate(board)
            board = zeroize(board)
            board = pullleft(board)
            board = rotate(board, False)
        return board